09 Metals: The nearly-free electron model

The nearly-free electron model is a modification of the free-electron gas model which includes a weak periodic perturbation meant to model the interaction between the conduction electrons and the ions in a crystalline solid. This model, like the free-electron model, does not take into account electron-electron interactions; that is, the independent-electron approximation is still in effect.

As shown by Bloch's theorem, introducing a periodic potential into the Schrödinger equation results in a wave function of the form

$\psi_{\bold{k}}(\bold{r}) = u_{\bold{k}}(\bold{r}) e^{i\bold{k}\cdot\bold{r}}$

where the function u has the same periodicity as the lattice:

$u_{\bold{k}}(\bold{r}) = u_{\bold{k}}(\bold{r}+\bold{T})$

(where T is a lattice translation vector.)

A solution of this form can be plugged into the Schrödinger equation, resulting in the central equation:

$(\lambda_{\bold{k}} - \epsilon)C_{\bold{k}} + \sum_{\bold{G}} U_{\bold{G}} C_{\bold{k}-\bold{G}}=0$

where

$\lambda_{\bold{k}} = \frac{\hbar^2 k^2}{2m}$

and C_k and U_G are the Fourier coefficients of the wavefunction ψ(r) and the potential energy U(r), respectively:

$U(\bold{r}) = \sum_{\bold{G}} U_{\bold{G}} e^{i\bold{G}\cdot\bold{r}}$

$\psi(\bold{r}) = \sum_{\bold{k}} C_{\bold{k}} e^{i\bold{k}\cdot\bold{r}}$

The vectors G are the reciprocal lattice vectors, and the discrete values of k are determined by the boundary conditions of the lattice under consideration.

In any perturbation analysis, one must consider the base case to which the perturbation is applied. Here, the base case is with U(x) = 0, and therefore all the Fourier coefficients of the potential are also zero. In this case the central equation reduces to the form

$(\lambda_{\bold{k}} - \epsilon)C_{\bold{k}} = 0$

This identity means that for each k, one of the two following cases must hold:

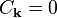$C_{\bold{k}} = 0$ ,
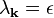
$\lambda_{\bold{k}} = \epsilon$

If the values of $λ k$ are non-degenerate, then the second case occurs for only one value of k, while for the rest, the Fourier expansion coefficient $C k$ must be zero. In this non-degenerate case, the standard free electron gas result is retrieved:

$\psi_k \propto e^{i\bold{k}\cdot\bold{r}}$

In the degenerate case, however, there will be a set of lattice vectors k₁, ..., k_m with λ₁ = ... = λ_m. When the energy $ε$ is equal to this value of λ, there will be m independent plane wave solutions of which any linear combination is also a solution:

$\psi \propto \sum_{i=1}^{m} A_i e^{i\bold{k}_i\cdot\bold{r}}$

Non-degenerate and degenerate perturbation theory can be applied in these two cases to solve for the Fourier coefficients C_k of the wavefunction (correct to first order in U) and the energy eigenvalue (correct to second order in U). An important result of this derivation is that there is no first-order shift in the energy ε in the case of no degeneracy, while there is in the case of near-degeneracy, implying that the latter case is more important in this analysis. Particularly, at the Brillouin zone boundary (or, equivalently, at any point on a Bragg plane), one finds a two-fold energy degeneracy that results in a shift in energy given by:

$\epsilon = \lambda_{\bold{k}} \pm |U_{\bold{k}}|$

This energy gap between Brillouin zones is known as the band gap, with a magnitude of $2 | U K |$ .

09 Metals

jueves, 29 de julio de 2010

The nearly-free electron model

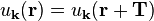
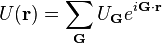
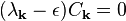
No hay comentarios:

Publicar un comentario